Question

The base of a right pyramid is a regular hexagon with sides of length 8m. The altitude is 4m. Find the total surface area of the pyramid.3√3/2*(8)²+3(8)*√[4²+3(8)²/4]The first part of the equation I calculate as 166.28, second part 192.00 for total 358.28. The correct answer on the review I'm studying for a test tonight has the correct answer as 192 + 96√3. How and why is 166.28 converted to 96√3? Thanks.

Answer 1

The total surface area is 192 + 96√3 m²

Step-by-step explanation

As you stated, the total surface area is the sum of the areas of each face of the pyramid.

96√3 is the area of the base of the pyramid, which is a regular hexagon with side length 8m:

`A_{\text{hex}}=\frac{3\sqrt[]{3}}{2}\cdot8^2=\frac{3\sqrt[]{3}\cdot64}{2}=3\sqrt[]{3}\cdot32=96\sqrt[]{3}m^2`

Then we have to look for the areas of the triangular faces of the pyramid

The area of each triangle is:

`A_{\text{triangle}}=(8\cdot h)/(2)`

To find the height we have to find the apothem of the hexagon first. Since we just found the area, we can use it to find the apothem, because the formula for the area of a regular hexagon also is:

`A_{\text{hex}}=(a\cdot P)/(2)`

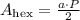
P is the perimeter, which is 6 times the side length:

`96\sqrt[]{3}=(a\cdot8\cdot6)/(2)`

Solving for a:

`a=\frac{96\sqrt[]{3}\cdot2}{8\cdot6}=\frac{\sqrt[]{3}\cdot192}{48}=4\sqrt[]{3}`

Now, using the Pythagorean theorem, we can find the height of the triangular face of the pyramid, which is the hypotenuse of the triangle formed by the height of the pyramid and the apothem of the hexagon:

`\begin{gathered} h=\sqrt[]{a^2+4^2}=\sqrt[]{(4\sqrt[]{3})^2+4^2} \\ h=\sqrt[]{16\cdot3+16} \\ h=\sqrt[]{48+16} \\ h=\sqrt[]{64} \\ h=8m \end{gathered}`

Therefore, the area of each triangular face is:

`A_{\text{triangle}}=(8\cdot8)/(2)=32m^2`

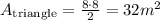
The total lateral surface area - i.e only the triangular faces - is:

`A_{\text{lateral}}=6\cdot A_{\text{triangle}}=6\cdot32m^2=192m^2`

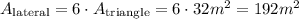
And the total surface area of the pyramid is the sum of the lateral area and the area of the base:

`SA=A_{\text{lateral}}+A_{\text{hex}}=192+96\sqrt[]{3}`