Question

A triangle has sides of lengths 27, 79, and 84. Is it a right triangle? Explain.

A.) yes. 27^2 + 79^2 = 84^2
B.) yes. 27^2 + 79^2 ≠ 84^2
C.) no. 27^2 + 79^2 = 84^2
D.) no. 27^2 + 79^2 ≠ 84^2

Answer 1

For a triangle to be right, it has to follow the Pythagorean theorem which states that,
c² = a² + b²
a and b are the shorter legs and c is the hypotenuse. From the given,
27² + 79² = 6970 ; 84² = 7056
They are not equal therefore, the answer is letter C.

Answer 2

No.

`27^2 + 79^2 \\eq 84^2`

Explanation:

For a triangle to be a right angle triangle:

The two shorter side squared need to add up to longest side squared.

Let a and b are the shortest side and c be the longest then;

You can use Pythagoras theorem;

`a^2+b^2=c^2`

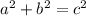
As per the statement:

A triangle has sides of lengths 27, 79, and 84

`29^2+79^2 = 729+6241 = 6970`

`84^2 = 7056`

then;

`29^2+79^2 \\eq 84^2`

Therefore, this violate the Pythagoras theorem;

therefore, this triangle is not a right angle triangle.