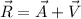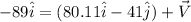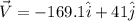Question

You are given a vector in the xy plane that has a magnitude of 90.0 units and, a y component of -41.0 units. Assuming the x component is known to be positive, specify the vector, V, if you add it to the original one, would give a resultant vector that is 89.0 units long and points entirely in the -x direction.

Answer 1

`\vec A = 80.11 \hat i - 41\hat j`

`\vec V = -169.1\hat i + 41\hat j`

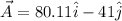
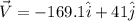
Step-by-step explanation:

Magnitude of the vector is 90 units

Y component of the vector is -41 units

Now we know that

`\vec A = x\hat i + y\hat j`

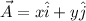
now the magnitude of vector A is given as

`A = √(x^2 + y^2)`

`90 = √(x^2 + 41^2)`

`90^2 = x^2 + 41^2`

`x = 80.11 units`

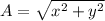
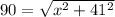
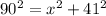
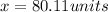
so the vector is given as

`\vec A = 80.11 \hat i - 41\hat j`

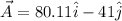
now Another vector V is added in it such that the resultant is 89 units and along - X direction

so we have

`\vec R = \vec A + \vec V`

`-89\hat i = (80.11\hat i - 41\hat j) + \vec V`

`-89\hat i - 80.11 \hat i + 41 \hat j = \vec V`

`\vec V = -169.1\hat i + 41\hat j`

Answer 2

In your question where as the given vector in the xy plane that has a magnitude of 90 units and a,y component of -41 units. So the vector V, base on my calculation and understanding in the problem, the value if it is (8.88, 41)