Question

What is the degree measure of an arc 4 ft. long in a circle of radius 10 ft.?

Answer 1

22.92 degrees.

Explanation:

We have been given that

s = 4 ft

r = 10 ft

We have to find the angle in degrees.

We know the relation

`\theta=(s)/(r)`

Here angle is in radians.

Substituting the values, we get

`\theta=(4)/(10)\\\\\theta=(2)/(5)\text{ radians}\\\\\theta=0.4\text{ radians}`

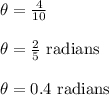
1 radian = 57.2958 degrees.

Hence, 0.4 radians = 22.92 degrees.

Therefore, the degree measure of the angle is 22.92 degrees.

Answer 2

The measure of the arc (S) given the angle it intercepted (A) and the radius is given by the equation,
S = (A / 360°) x (2πr)
Substituting the values to the equation above,
4 ft = (A / 360°) x (2π)(10 ft)
The value of A is 22.92°.