Question

Anne currently brings in an annual salary of $37,184 and anticipates a raise of6% every year. What will her salary be in 13 years? Round your answer to the nearest dollar.

Answer 1

We are given that the amount $37184 will increase by a percentage of 6% every year. This can be modeled using an equation of exponential growth, which follows the next function:

`y=P_0(1+r)^t`

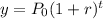
Where:

`\begin{gathered} P_0=\text{ initial value} \\ r=\text{ growth rate} \\ t=\text{ time} \end{gathered}`

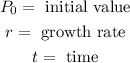
The initial value is:

`P_0=37184`

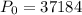
The growth rate must be in decimal form. To obtain the decimal form we divide the percentage rate by 100:

`r=(6)/(100)=0.06`

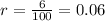
Now, we substitute the values:

`y=37184(1+0.06^{})^t`

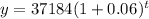
Now, we solve the operations inside the parenthesis:

`y=37184(1.06)^t`

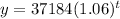
Now, we substitute the value of "t = 13", we get:

`y=37184(1.06)^(13)`

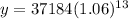
Solving the operations:

`y=79311`

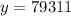
Therefore, her salary in 13 years will be $79311