Question

1. A standard number cube is tossed. Find P(even or prime).1. 5/62. 1/23. 2/34. 1/6

Answer 1

Given: A standard number cube is tossed

To determine: The P(even or prime)

Solution

Step 1: Write the element of the sample space

`\begin{gathered} S=\mleft\lbrace1,2,3,4,5,6\mright\rbrace \\ n(S)=6 \end{gathered}`

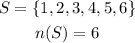
Step 2: Write the element of even

`\begin{gathered} evennumber=\mleft\lbrace_{}2,4,6\mright\rbrace \\ n(\text{even)}=3 \end{gathered}`

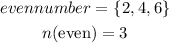
Step 3: Write the elemt of prime

`\begin{gathered} prime\text{ number=}\mleft\lbrace2,3,5\mright\rbrace \\ n(prime\text{)}=3 \end{gathered}`

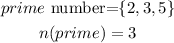
Step 4: Write element of even and prime

`(\text{odd}\cap even)=\mleft\lbrace2\mright\rbrace`

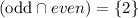
Step 5: Find the P(even or prime)

`P_{(\text{even or odd)}}=P(even)+P(odd)-P(odd\cap even)`
`\begin{gathered} P(\text{even)}=(3)/(6) \\ P(\text{prime)}=(3)/(6) \\ P(\text{even }\cap prime)=(3)/(6)+(3)/(6)-(1)/(6) \\ P(\text{even }\cap prime)=(3+3-1)/(6) \\ P(\text{even }\cap prime)=(5)/(6) \end{gathered}`

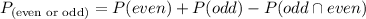
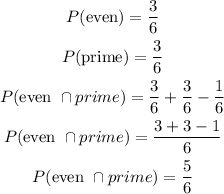
Hence, the probability of even and odd is 5/6