Question

question provided in picture Just B, C and D(c)What is the probability of not being awakened if the student uses three independent alarm clocks (round to five decimal places as needed)

Answer 1

• (a)0.123

,

• (b)0.01513

,

• (c)0.00186

,

• (d)Option C

Explanation:

Part A

The clock has a 12.3% failure rate. Therefore, the probability that the student's alarm clock will not work on the morning= 0.123

Part B

If the student has two such alarm clocks, the probability that they both fail:

`\begin{gathered} P(\text{both fail)=P(1st fail AND second fail)} \\ =P(1st\text{ fail)}* P(\sec ond\text{ fail)} \\ =0.123*0.123 \\ \approx0.01513 \end{gathered}`

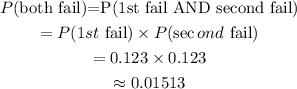
The probability that the two clocks fail is 0.01513 (correct to 5 decimal places).

Part C

If the student uses three independent alarm clocks and is not awakened, it meant that the three alarm clocks failed.

Therefore, the probability of not being awakened is:

`\begin{gathered} P(\text{not being awaked)=P(1st fail AND second fail AND third fail)} \\ =P(1st\text{ fail)}* P(\sec ond\text{ fail)}* P(third\text{ fail)} \\ =0.123*0.123*0.123 \\ \approx0.00186 \end{gathered}`

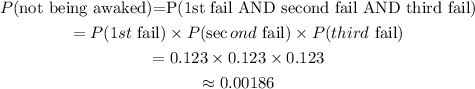
The probability of not being awakened is 0.00186 (correct to 5 decimal places).

Part D

For each extra clock, the probability of malfunctions becomes smaller. Thus, becoming very unlikely.

Therefore, the correct answer is:

(C) ​Yes, because total malfunction would not be​ impossible, but it would be unlikely.