Question

how does the volume of a rectangular prism change if the the width is reduced to 1/10 of its original size, the height is reduced to 1/4 of its original size, and the length is reduced to 2/3 of its original size?

Answer 1

V=1/60lwh let me know if it helped

Answer 2

Answer: The new volume will be
`(1)/(60)` of the original volume.

Step-by-step explanation: Given that the width of rectangular prism is reduced to one-tenth of its original size, the height is reduced to one-fourth of its original size and the length is reduced to two-third of its original size.

We are to find the change in the volume of the prism.

We know that

the VOLUME of a rectangular prism with width w units, height h units and length l units is given by

`V=whl.`

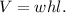
Now, after change in the dimensions as given, the new dimensions of the rectangular prism will be

`w'=(w)/(10),~~h'=(h)/(4),~~l=(2l)/(3).`

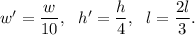
Therefore, the new VOLUME of the prism will be

`V'=w'h'l'=(w)/(10)*(h)/(4)*(2l)/(3)=(1)/(60)* whl=(1)/(60)* V.`

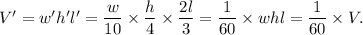
Thus, the new volume will be
`(1)/(60)` of the original volume.