Question

H(t) = –16t2 + 14t find the maximum height

Answer 1

The height is represented as y and the time is represented as x.


To find the maximum height (since this is a parabola that faces downwards) we need to find the vertex.


Vertex (x) =
`(-(b))/(2a)`

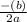
b = 14
a = -16

Substitute

`(-14)/(2(-16)) = (-14)/(-32) = (7)/(8)`

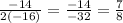
Now plug 7/8 to t
-16(7/8)^2 + 14(7/8)
-16(49/64) + 14(7/8)
-12.25 + 12.25
Answer: 0 ft

Answer 2

I suppouse the height is in meters and the time is in seconds.

1) we calculate the first derivative:
H´(t)=-32t+14

2) we math the first derivative to "0"; and we find out the value of "X".
-32t+14=0
t=-14/-32
t=7/16

3) we calculate the second derivative:
H´´(t)=-32<0; then at t=7/16 we have a maximum.

4) we find out the maximun height.

H(7/16)=-16(7/16)²+14(7/16)
H(7/16)=-3.0625+6.125
H(7/16)=3.0625≈3.063

Answer: the maximun height was 3.063 m.


If the height is in ft; then the answer is 3.063 ft.