Answer:
The coordinates of the turning point will be (-2, -4)
Explanation:
The given function is
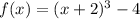
The turning point is a point where the function goes from increasing to decreasing or reciprocally.
At the point where the gradient or slope of the curve is 0, that is the turning point.
Gradient is the first derivative of the function.
so,
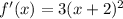
Then,
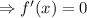
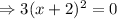
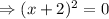
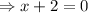
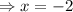
At x= -2, f(x) will be
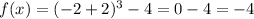
So the coordinates of the turning point will be (-2, -4)