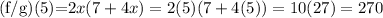Question

If c(x)=5/x-2 and d(x)=x+3 what is the domain of (cd)(x)?. . And, if f(x)=7+4x and g(x)=1/2x, what is the value of (f/g)(5)?

Answer 1

Domain of (cd)(x) is all real numbers values except 2.

The value of (f/g)(5) is 270

Explanation:

Given c(x) and d(x) we have to find the domain of (cd)(x)

`c(x)=(5)/(x)-2` and
`d(x)=x+3`

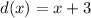
The product of above two is

`(cd)(x)=c(x)d(x)=((5)/(x-2))(x+3)`

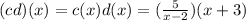
The above function is defined at all real numbers values except 2 because that would make the denominator 0.

Hence, domain of (cd)(x) is all real numbers except 2.

Given
`f(x)=7+4x` and
`g(x)=(1)/(2x)`

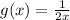
we have to find the value of (f/g)(5)

`\text{(f/g)x=}(7+4x)/((1)/(2x))=2x(7+4x)`

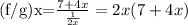
put x=5

`\text{(f/g)(5)=}2x(7+4x)=2(5)(7+4(5))=10(27)=270`

Answer 2

1. The value of (cd)(x) is equal to the product of c(x) and d(x) which is equal to,
5(x + 3) / (x - 2)
The function can take all real numbers except 2 because that would make the denominator 0.

2. To answer, substitute first 5 to the given functions,
f(x) = 7 + 4x = 7 + 4(5) = 27
g(x) = 1/2x = 1 / (2)(5) = 1/10
Dividing 27 by 1/10 is 270.