Question

Megan’s TV had a base price of $189 and the sales tax was 6.88%. Over the next four years, the TV consumed an average of $0.06 of electricity every day. It also needed repairs twice, costing $29 each time. After four years, Megan got a new TV. What was the lifetime cost of Megan’s TV? (Remember that one in every four years is a leap year.)

Answer 1

The solution would be like this for this specific problem:

189 x .0688 = 12.8 + 189 = 201.8
(4 x 360) x .06 = 86.4
(29 x 2) + 86.4 = 144.4
201.8 + 144.4 = $346.2

I am hoping that this answer has satisfied your query and it will be able to help you in your endeavor, and if you would like, feel free to ask another question.

Answer 2

lifetime cost of the Megans TV is $347 .66 .

Explanation:

As given

Megan’s TV had a base price of $189 and the sales tax was 6.88%.

6.88 % is written in the decimal form.

`= (6.88)/(100)`

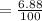
= 0.0688

Sales tax price = 0.0688 × Base price

= 0.0688 × 189

= $ 13 (Approx)

As given

Over the next four years, the TV consumed an average of $0.06 of electricity every day.

As 1 year contains 365 days and a leap year contains 366 days .

Thus

Electricity consumed in four years = Average electricity × (3× Number of days in one years + Number of days in a leap year )

= 0.06 × ( 3 × 365 + 366)

= 0.06 × (1095 + 366)

= 0.06 × 1461

= 87.66

As given

It also needed repairs twice, costing $29 each time.

Repair cost = 2 × Cost of repair

= 2 × 29

= $58

Thus

Lifetime cost of the Megans TV = Base cost + Sales price cost + Electricity consumed in four years + Repair cost .

Putting all the values in the above

Lifetime cost of the Megans TV = $189 + $13 + $87.66 + $ 58

= $ 347.66

Therefore the lifetime cost of the Megans TV is $347 .66 .