Question

A sphere has a diameter of 14 units. What is the volume of the sphere in cubic units? If a cylinder has the same radius as the sphere and a height of 14 units, what is the volume of the cylinder? Use 3.14 for π.

Answer 1

see the attachment for answer:
V≈1436.76 units cube (sphere)
V=πr^2h (cylinder)
r=7
h=14

V≈2155.13 units cube (cylinder)

Answer 2

`\text{Volume of sphere}\approx 1436.03` cubic units.

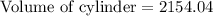`\text{Volume of cylinder}=2154.04` cubic units.

Explanation:

We have been given that a sphere has a diameter of 14 units. We are asked to find the volume of our given sphere.

`\text{Volume of sphere}=(4)/(3)\pi r^3`, where r represents the radius of sphere.

First of all, let us divide the diameter of sphere by 2 to find the radius of our given sphere.

`\text{Radius of sphere}=(14)/(2)=7`

`\text{Volume of sphere}=(4)/(3)*3.14*7^3`

`\text{Volume of sphere}=(4)/(3)*3.14*343`

`\text{Volume of sphere}=(4308.08)/(3)`

`\text{Volume of sphere}=1436.02666\approx 1436.03`

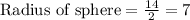
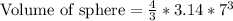
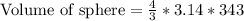
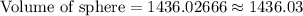
Therefore, the volume of sphere is 1436.03 cubic units.

`\text{Volume of cylinder}=\pi r^2h`, where,

r = Radius of cylinder,

h = Height of cylinder.

Upon substituting our given values in above formula we will get,

`\text{Volume of cylinder}=\pi*7^2*14`

`\text{Volume of cylinder}=3.14*49*14`

`\text{Volume of cylinder}=2154.04`

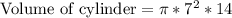
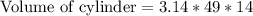
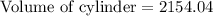
Therefore, the volume of cylinder is 2154.04 cubic units.