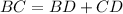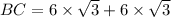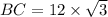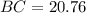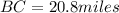Question

While crossing the Atlantic, sailors spot two mermaids 120° apart on each end of an island that is 6 miles away. How far apart are the mermaids around the outer edge of the island to the nearest tenth of a mile?

Answer 1

The question specified that the two mermaids (assuming the sailors wernt just flat out drunk and were just seeing things) were on either side of the island, 120 degrees apart from each other, meaning that each one of them are 60 degrees (half of 120) from the island. The distance between one mermaid and the island, if you draw out the diagram properly, should be s=6*tan(60 degrees)=6tan(pi/3)=6*sqrt(3). The distance between the two mermaids is then simply 2s = 12sqrt(3)

Answer 2

outer edge of the island is 20.8 miles

Explanation:

As shown in figure sailor spot two mermaids at point B and C. BC is the outer edge of island. Point A represents sailors

AD=6 miles is perpendicular bisector of BC.

It is clear that

`\angle A=120 $^(\circ)$`

and

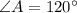
`\angle BAD=\angle CAD=60$^(\circ)$`

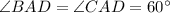
we will find BD and DC

in
`\triangle BAD`

`tan 60$^(\circ)$`=
`(BD)/(AD)`

`\sqrt 3=(BD)/(6)`

`BD=6* \sqrt 3`

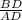
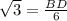
Similarly, in
`\triangle CAD`

`tan 60$^(\circ)$`=
`(CD)/(AD)`

`\sqrt 3=(CD)/(6)`

`CD=6* \sqrt 3`

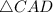
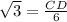
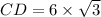
Therefore outer edge of the island,

`BC=BD+CD`

`BC=6* \sqrt 3+6* \sqrt 3`

`BC=12* \sqrt 3`

`BC=12* 1.73`

`BC=20.76`

`BC=20.8 miles`