Question

Find the quotient. Show all work for full credit.

Answer 1

2.2 - 0.4
`i`

Explanation:

1. Approach

To divide by imaginary number, one must take the fraction and multiply the complex conjugate of the denominator. A complex conjugate is a complex number with its imaginary unit multiplied by (-1). Once one multiplies both the numerator and denominator by the complex conjugate, then the denominator should be a real number (this is because the complex numbers act like binomials when multiplied, and hence the difference of square property works). Now all one has to do is divide every term in the numerator by the real number in the denominator.

2. complex conjugate

As mentioned above, to solve this problem, one has to multiply the numerator and denominator by the complex conjugate of the denominator. That is the complex number in the denominator with its imaginary until multiplied by (-1).

Complex number in the denominator;

(-8 - 6i)

complex conjugate;

(-8 + 6i)

3. Multiplying

Now, one has to multiply the problem's numerator and denominator by the complex conjugate of the denominator. Since a number over itself in fraction format is the same as multiplying by (1), one is allowed to do this;

`(-2-i)/(-8-6i)`

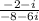
Multiply

`(-2-i)/(-8-6i) * (-8+6i)/(-8+6i)`

Distribute

`((-2)(-8) + (-2)(6i) + (-i)(-8) + (-i)(6i))/((-8)(-8)+(-8)(6i) + (-6i)(-8) + (-6i)(6i))`

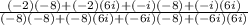
4. Simplifying

Now all that is left is to simplify and divide to find the quotient.

=
`((-2)(-8) + (-2)(6i) + (-i)(-8) + (-i)(6i))/((-8)(-8)+(-8)(6i) + (-6i)(-8) + (-6i)(6i))`

=
`(16 - 12i +8i -6i^(2))/(64-48i+48i-36i^(2))`

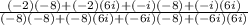
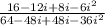
Remember the rotations of
`i`,
`i^(2) = -1`

Simplify further

`(16-4i+6)/(64+36)\\\\=(22-4i)/(100)`

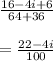
Divide

2.2 - 0.4
`i`