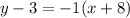Question

The equations are written in point-slope form. Which equation represents a line through points (–8, 3) and (–2, –3)?

y-3=-3(x+8)
y-3=3(x+8)
y-3=1(x+8)
y-3=-1(x+8)

Answer 1

(-8,3)(-2,-3)
slope(m) = (-3-3) / (-2 - (-8) = -6/6 = -1

y - y1 = m(x - x1)
slope(m) = -1
(-8,3)...x1 = -8 and y1 = 3
now we sub
y - 3 = -1(x - (-8) =
y - 3 = -1(x + 8)

Answer 2

Option 4th is correct

`y-3 = -1(x+8)`

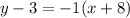
Explanation:

Point-slope intercept form:

The equation of straight line is given by:

`y-y_1 = m(x-x_1)` .....[1]

where, m is the slope and
`(x_1, y_1)` is the point on the line.

As per the statement:

A line through points (–8, 3) and (–2, –3).

Formula for slope is given by:

`\text{Slope (m)} = (y_2-y_1)/(x_2-x_1)`

Substitute the given points we have;

`m = (-3-3)/(-2-(-8)) = (-6)/(-2+8)=(-6)/(6) = -1`

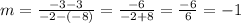
Substitute the given value of m = -1 and (-8, 3) in [1] we have;

`y-3 = -1(x-(-8))`

⇒
`y-3 = -1(x+8)`

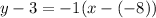
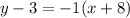
Therefore, the equations represents a line through points (–8, 3) and (–2, –3) is,
`y-3 = -1(x+8)`