Question

A motorist drives north for 36.0 minutes at 69.5 km/h and then stops for 15.0 minutes. He then continues north, traveling 130 km in 1.60 h.(a) What is his total displacement? km(b) What is his average velocity? km/h

Answer 1

a)

Since all the displacement is made towards north we don't need to worry about signs on the velocity which we know is given by:

`v=(\Delta x)/(\Delta t)`

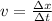
For the first part of the motion we know that the motorist drove north for 36 minutes at 69.5 km/h, to determine the displacement we first need to convert the time to hours:

`36\text{ min}\cdot\frac{1\text{ h}}{60\text{ min}}=0.6\text{ h}`

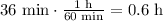
Then for the first part we have:

`\begin{gathered} 69.5=(\Delta x)/(0.6) \\ \Delta x=(0.6)(69.5) \\ \Delta x=41.7 \end{gathered}`

hence, for the first part the motorist displacement was 41.7 km.

For the second part we know he traveled 130 km, to find the total displacement we just add it to the previous result:

`\Delta x=41.7+130=171.7`

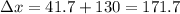
Therefore, the total displacement is 171.7 km.

b)

We know the total displacement of the motorist, to find the velocity we need to determine the total time it took, adding the times for each part of the trip we have:

`0.6+(15)/(60)+1.6=2.45`

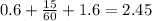
Then we have:

`\begin{gathered} v=(171.7)/(2.45) \\ v=70.1 \end{gathered}`

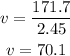
Therefore, the average velocity is 70.1 km/h