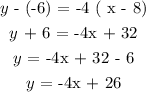Answer:
The equation of the line is y = -4x + 26
Explanations:
The slope-intercept form of the equation of a line is:
y = mx + c
where m = the slope
c = the y-intercept
Comparing the given equation y = 1/4 x + 3 with y = mx + c
m = 1/4
c = 3
The point-slope equation of the line perpendicular to the line y = mx + c is given as:
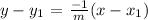
Since the line passes through the point (8, -6)
x₁ = 8, y₁ = -6
-1/m = -1/(1/4) = -4
Substituting the values of x₁, y₁, and -1/m into the equation above: