Question

A rectangle is drawn so the width is 2 inches longer than the height. If the rectangle's diagonal measurement is 28 inches, find the height.Give your answer rounded to 1 decimal place.

Answer 1

We have a rectangle that has a width that is 2 inches longer than its height.

We know that the diagonal is 28 inches long.

We can draw this as:

We can use the Pythagorean theorem to relate the measures as:

`\begin{gathered} h^2+w^2=d^2 \\ h^2+(h+2)^2=28^2 \\ h^2+h^2+4h+4=784 \\ 2h^2+4h+4-784=0 \\ 2h^2+4h-780=0 \\ h^2+2h-390=0 \end{gathered}`

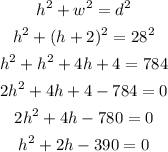
The height will come from the solution of this quadratic equation:

`\begin{gathered} h=(-2\pm√(2^2-4\cdot1\cdot(-390)))/(2\cdot1) \\ \\ h=(-2\pm√(4+1560))/(2) \\ \\ h=(-2\pm√(1564))/(2) \\ \\ h=(-2\pm39.547)/(2) \\ \\ h=-1\pm19.77 \\ \Rightarrow h_1=-1-19.77=-20.77 \\ \Rightarrow h_2=-1+19.77=18.77 \end{gathered}`

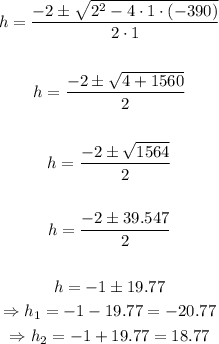
The negative solution does not make sense in the context of the problem, so the solution to this problem is h = 18.8 inches.

Answer: the height is approximately 18.8 inches.