Question

Suppose that F(x) = x3 and G(x) = -2x3 - 7. Which statement best compares the graph of G(x) with the graph of F(x)?

Answer 1

As per the statement given that
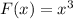`F(x) = x^3` and
`G(x) = -2x^3-7`

⇒ Let the parent function be
`F(x) = x^3`

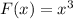
Vertically Stretch: If y =f(x) , then y = a f(x) gives a vertical stretch if a> 1.

Rotation about x -axis:
`(x, y) \rightarrow (x, -y)`

Shifting down: To shift a graph down some units c, we will be subtracting outside the function: y= f(x)-c.

Just Multiplying the parent function by 2 means you are stretching it vertically,

i,e F(x) =
`x^3 \rightarrow \text{Vertically stretch by 2} \rightarrow 2x^3`

adding the minus sign means you are flipping or rotating it about the x-axis

i,e
`2x^3 \rightarrow \text{Rotation about x- axis} \rightarrow -2x^3`

and subtracting 7 means you are moving it down by 7 units

`-2x^3 \rightarrow \text{Shifted down by 7 units} \rightarrow -2x^3-7` =G(x)

Therefore, the statement best compare the graph G(x) with the graph of F(x)

the graph of G(x) is the graph of F(x) stretched vertically by 2 units, flipped over the x-axis, and shifted 7 units down.