Question

The first equation in the system models the heights, h, of a falling volleyball as a function of time, t. The second equation models the heights, h, of the hands of a player jumping up to spike the ball as a function of time, t. Which statement describes the situation modeled by this system?

h=14-16t^2
h=7+24t-16t^2
A.The volleyball is 7 feet above the ground at the instant the player begins her jump.
B.The volleyball is 14 feet above the ground at the instant the player begins her jump.
C.The volleyball is 16 feet above the ground at the instant the player begins her jump.
D.The volleyball is 24 feet above the ground at the instant the player begins her jump.
FIRST PERSON TO ANSWER GETS A THANKS NEED HELP ASAP

Answer 1

Hello,

In red : the falling volleyball h_1=14-16t^2

In Bleue : the player's jump h_2=7+24t-16t^2

If t=0 h_1=14

Answer 2

The volleyball is 14 feet above the ground at the instant the pl;ayer begins her jump.

B is correct.

Explanation:

Here we have two situation of system of models.

`\text{The height (h) of a falling volleyball as function of time (t):}h(t)=14-16t^2`

`\text{The height (h) of the hands of a player as function of time (t):}h(t)=7+24t-16t^2`

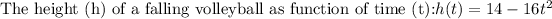
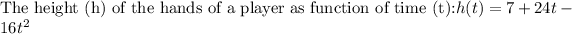
We need to find the height of ball above the ground at the instant the player begins jump.

At t=0, player begins jump.

We put t=0 into
`h(t)=7+24t-16t^2`

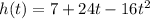
Height of player hand at t=0 , h=7 feet.

Now we will set t=0 for first model.

`h(0)=14-16* 0^2\Rightarrow 14`

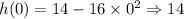
Thus, The volleyball is 14 feet above the ground at the instant the pl;ayer begins her jump.

B is correct.