Question

The angle looking up at the sun is 70°. A flagpole casts a shadow of 15 ft. Draw a diagram and find the height of the flagpole

A) 41.2 ft.
B) 14.1 ft
C) 5.5 ft

Answer 1

Option A is correct

the height of the flagpole is, 41.2 ft

Explanation:

As per the statement:

The angle looking up at the sun is 70°

⇒
`\theta= 70^(\circ)`

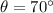
It is also given that:

A flagpole casts a shadow of 15 ft.

For this you can see the diagram as shown below in the attachment.

Now, find the height of the flagpole.

Let h be the height of flagpole.

using tangent ratio:

`\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}`

From the given diagram;

`\theta = 70^(\circ)`

Opposite side = Height of the Flag pole = h

Adjacent side = Shadow of the flagpole = 15 ft

Substitute these we get;

`\tan 70^(\circ) = (h)/(15)`

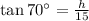
Multiply both sides by 15 we get;

`15 \cdot \tan 70^(\circ) = h`

`15 \cdot 2.75 = h`

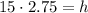
Simplify:

`41.2 ft = h`

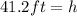
or

h = 41.2 ft

Therefore, the height of the flagpole is, 41.2 ft

Answer 2

The length of the flagpole be 41.2 ft .

Option (A) is correct .

Explanation:

As given

The angle looking up at the sun is 70°.

A flagpole casts a shadow of 15 ft .

Now by using the trignometric identity .

`tan \theta = (Perpendicular)/(Base)`

`\ theta = 70^(\circ)`

`tan\ 70^(\circ) = (AB)/(BC)`

BC = 15 ft

tan 70° = 2.75 (Approx)

`2.75 = (AB)/(15)`

AB = 2.75 × 15

= 41.2 ft

Therefore the length of the flagpole be 41.2 ft .

Option (A) is correct .