Question

1. If ƒ (x ) = 2x^2 + 3, find ƒ (3).

2. Simplify.
(x 3)^4 • x^-3

3. Simplify.
8 - 3(4 - 2x )

4.
If ƒ (x ) = 4x - 3, what is ƒ (x )^-1?

5.
if ƒ = {(2, 5), (3, 2) (4, 6), (5, 1), (7, 2)}, then ƒ is a function.

Answer 1

1. f(3)= 2(3^2)+3 = 21
2. Do you mean (x+3)^4 X x^-3 ?
3. 8-12+6x= 6x-4
4. (4x-3)^-1 = 1/(4x-3)
5. So whats the question for 5?

Answer 2

`f(3)=21`

`(x^3)^4.x^(-3)=x^(9)`

`8-3(4-2x)=6x-4`

`f^(-1)(x)=(1)/(4)(x+3)`

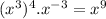
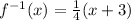
f = {(2, 5), (3, 2) (4, 6), (5, 1), (7, 2)} is a function

Explanation:

`\text{Part 1: Given the function }f(x)=2x^2+3`

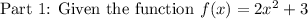
we have to find the value of f(3)

`f(x)=2x^2+3`

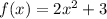
Substitute x=3

`f(3)=2(3)^2+3=2* 9+3=18+3=21`

`\text{Part 2: Given the expression }(x^3)^4.x^(-3)`

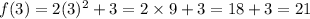
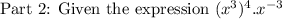
we have to simplify the above expression

`(x^3)^4.x^(-3)`

`=x^(3* 4).x^(-3)`

`=x^(12).x^(-3)`

`=x^(12-3)=x^(9)`

`\text{Part 3: Given the expression }8-3(4-2x)`

`8-3(4-2x)`

`=8-(12-6x)`

`=8-12+6x=6x-4`

`\text{Part 4:Given the function }f(x)=4x-3`

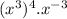
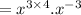
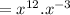
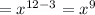
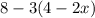
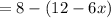
we have to find the
`f^(-1)(x)`

Replace f(x) to y

`y=4x-3`

To find inverse we have to replace x=y and y=x, we get

`x=4y-3`

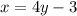
Now solve for y and replace y with
`f^(-1)(x)`

`x+3=4y`

`y=(1)/(4)(x+3)`

`f^(-1)(x)=(1)/(4)(x+3)`

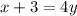
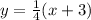
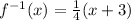
which is required inverse

`\text{Part 5: If f = {(2, 5), (3, 2) (4, 6), (5, 1), (7, 2)},}`

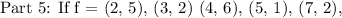
we have to find f is function or not.

If one element of domain x has unique image in range i.e in Y set then only f is called function.

Here one maps to unique element

Therefore f is function.