Answer:
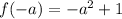
Explanation:
We have been a function
 . We are asked to simplify our function at the indicated value
. We are asked to simplify our function at the indicated value
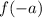 .
.
To find
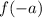 for our given function, we will substitute
for our given function, we will substitute
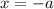 in our given function as:
in our given function as:
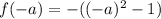
We know that a negative number raised to an even power results in positive, so our function would be:
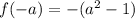
Using distributive property
 , we will get:
, we will get:
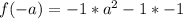
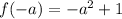
Therefore, the value of
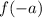 is
is
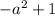 .
.