Question

In sunlight, a vertical yardstick casts a 1 ft shadow at the same time that a nearby tree casts a 15 ft shadow. How tall is the tree?

Answer 1

Tree is 45 ft tall.

Explanation:

In the figure attached AB is the tree and CD is the yardstick.

Shadow of tree AB is BO = 15 ft and shadow of yardstick is CO.

since length of a yardstick is = 1 yard or 3 ft.

Now we know that ΔABO and ΔDCO are similar.(since ∠A = ∠D and ∠B = ∠C = 90° so AA property proving triangles similar)

Therefore
`(AB)/(CD)=(OB)/(OC)`

By putting the values of AB and CD

`(x)/(3)=(15)/(1)`

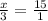
x = 3×15 = 45 ft.

Therefore the height of the tree is 45 ft.

Answer 2

To answer this specific problem, the tree is 45 feet tall. I am hoping that this answer has satisfied your query and it will be able to help you, and if you would like, feel free to ask another question.