Question

Give an example of a function with both a removable and a non-removable discontinuity..

Answer 1

In your question to determine if a function is both a removable and non removable discontinuity is to get the value of its variable either its graph has hole and also it will jump or its an asymptote in the graph. The best example to this is f(x)=x−1(x−1)(x−2)f(x)=x−1(x−1)(x−2)

Answer 2

`f(x)=(x+1)/((x+1)(x-2))`and f(-1) =1

Removable discontinuity at x=-1 and non removable discontinuity at x =2

Explanation:

Removable discontinuity:When a function is not defined at one point and all other points function is defined .Then the point is called removable discontinuity.In this function, limit exist but value of function at x=a is not equal to the value of function after applying limit.

`\lim_(x\rightarrow a)f(x)\\eq f(a)`

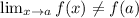
Non- removable discontinuity:It can not be removed .The point at which function can not be defined and denominator x is zero for corresponding value of x .The limit of function at x= a does not exist .Left hand limit and right hand limit both are exist but they are not equal.Then , we say function have non removable discontinuity.

For example

`f(x)=(x+1)/((x+1)(x-2))` and f(-1) =1

The given function have removable discontinuity at x= -1 and at x=2 , function have non - removable discontinuity .