Question

Which of the following represent the zeros of f(x) = 6x^3 – 29x^2 – 6x + 5. . 5, 1/3, -1/2. . 5, -1/3, 1/2. . -5, 1/3, -1/2,. . 5, 1/3, 1/2

Answer 1

the zeros of the equation 6x^3 – 29x^2 – 6x + 5 can be determined using the calculator. The number of roots of the equation is equal to the highest degree among the terms in the polynomial. In this case, there are 3 roots. Using the calculator, the roots are 5, 1/3, and -1/2. Answer is A.

Answer 2

For the polynomial
`f(x) = 6x^3 - 29x^2 - 6x + 5` you can determine the possible rational zeroes as fraction c/d, where c and d are integer numbers that are respectively, divisors of 5 (the last coefficient) and 6 (the first coefficient).

Divisors of 5:
`\pm 1, \pm 5;`

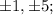
Divisors of 6:
`\pm 1, \pm 2, \pm 3, \pm 6.`

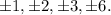
Then zeros can be among fractions:

`\pm(1)/(1)=\pm 1; \pm(1)/(2); \pm(1)/(3); \pm(1)/(6); \pm(5)/(1)=\pm 5; \pm(5)/(2); \pm(5)/(3); \pm(5)/(6).`

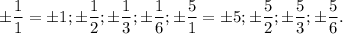
You can use syntetic division to determine which fractions fit, or you can simply count:

`f(5)=6\cdot 5^3 - 29\cdot 5^2 - 6\cdot 5 + 5=750-725-30+5=0` this means that x=5 is a polynomial zero.

Then

`f(x) = 6x^3 - 29x^2 - 6x + 5=(x-5)(6x^2+x-1).`

Trinomial
`6x^2+x-1` is quadratic, then
`6x^2+x-1=6(x-x_1)(x-x_2)=6(x+(1)/(2))(x-(1)/(3))`

and

`f(x) = 6x^3 - 29x^2 - 6x + 5=6(x-5)(x+(1)/(2))(x-(1)/(3)) .`

Zeros are
`5, -(1)/(2), (1)/(3) .`

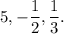
Answer: correct choice is A.