Question

Irina wants to build a fence around a rectangular vegetable garden so that it has a width of at least 10 feet. She can use a maximum of 150 feet of

fencing. The system of inequalities that models the possible lengths, l, and widths, w, of her garden is shown.


w ≥ 10

2l + 2w ≤ 150



a = 20 ft; w = 5 ft


b= 20 ft; w = 10 ft


c = 60 ft; w = 20 ft


d = 55 ft; w = 30 ft

Answer 1

Answer: Only Option 2 is correct.

Explanation:

Since we have given that

Rectangular vegetable garden has width of at least 10 feet i.e.

`w\geq 10`

She can use a maximum of 150 feet of fencing.

i.e.

`Perimeter\leq 150\\\\2(l+w)\leq 150\\\\2l+2w\leq 150`

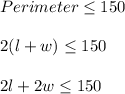
So, Option 1 get rejected as it has w = 5 which less than 1. But width has at least 10 feet.

Option 2) b= 20 ft; w = 10 ft

`\\\\2* 20+2* 10\leq 150\\\\40+20\leq 150\\\\60\leq 150\\\\True.`

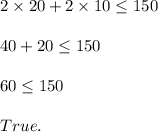
Option 3) c = 60 ft; w = 20 ft

`\\\\2* 60+2* 20\leq 150\\\\120+40\leq 150\\\\160>150\\\\False.`

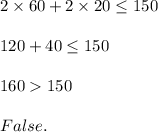
Option 4) d = 55 ft; w = 30 ft

`\\\\2* 55+2* 30\leq 150\\\\110+60\leq 150\\\\170>150\\\\False.`

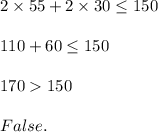
Hence, only Option 2 is correct.

Answer 2

In option a, w < 10
in option b, w = 10 and 2(20) + 2(10) = 40 + 20 = 60 < 150
in option c, w > 10 but 2(60) + 2(20) = 120 + 40 = 160 > 150
In option d, w > 10 but 2(55) + 2(30) = 110 + 60 = 170 > 150

Therefore the corect answer is option b.