Question

use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the y-axis. y=8-x^2,y=x^2,x=0

Answer 1

16π square units.

Explanation:

Please refer to the graph below.

So, if we draw a representative rectangle, the width of the rectangle will be (x), and the height of the rectangle at each (x) will be given by f(x) - g(x).

By the shell method:

`\displaystyle V=2\pi\int_a^bp(x)h(x)\,dx`

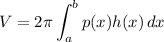
We are integrating from x = 0 to x = 2. p(x) is x and h(x) is f(x) - g(x):

`\displaystyle V=2\pi\int_0^2(x)((8-x^2)-(x^2))\,dx`

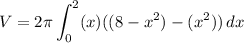
Evaluate. Simplify:

`\displaystyle V=2\pi \int_0^2(8x-2x^3)\,dx`

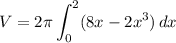
Hence:

`\displaystyle V=2\pi\Big(4x^2-(1)/(2)x^4\Big|_(0)^(2)\Big)`

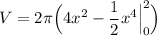
Evaluate:

`\displaystyle \begin{aligned} V &= 2 \pi \Big[(4(2)^2-(1)/(2)(2)^4)-(4(0)^2-(1)/(2)(0)^4)\Big]\\ &=2\pi(8) \\&=16\pi\text{ square units} \end{aligned}`