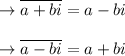Question

Find the quotient. write your answer in standard form 3-i/3+i

Answer 1

`(3-i)/(3+i)=((3-i)(3-i))/((3+i)(3-i)^((*)))=((3)(3)-(3)(i)-(i)(3)+(i)(i)^((**)))/(3^2-i^2^((**)))\\\\=(9-3i-3i-1)/(9-(-1))=(8-6i)/(9+1)=(8-6i)/(10)=(2(4-3i))/(2\cdot5)=\boxed{(4-3i)/(5)}\\\\\boxed{\boxed{(4)/(5)-(3)/(5)i}}`

Answer 2

Answer with explanation:

`(3-i)/(3+i)\\\\=((3-i)*(3-i))/((3+i)*(3-i))\\\\=((3-i)^2)/(3^2-(i)^2)\\\\=(3^2+i^2-2 * 3 * i)/(9-(-1))\\\\=(9-1-6 i)/(9+1)\\\\=(8-6 i)/(10)\\\\=(8)/(10)-(6 i)/(10)\\\\=(4)/(5)-(3i)/(5)`

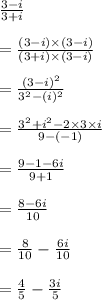
⇒To write a complex number in standard form,having complex number in it's denominator multiply by it's conjugate in numerator and denominator

Used the following identities to solve the complex number in fractional form

→ (a+bi)(a-bi)=a²+b²

→i=√-1, i²= -1

`\rightarrow{\overline{a+bi}}=a-b i\\\\\rightarrow{\overline{a-bi}}=a+bi`