Question

Solve for X:7x-30<-5(3-2x)

Answer 1

x > - 5

Step-by-step explanation:

The initial expression is:

`7x-30<-5(3-2x)`

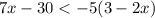
First, we can apply distributive property on the right side as follows:

`\begin{gathered} 7x-30<-5\cdot3-5(-2x) \\ 7x-30<-15+10x \end{gathered}`

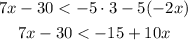
Now, we can add 30 to both sides:

`\begin{gathered} 7x-30+30<-15+10x+30 \\ 7x<15+10x \end{gathered}`

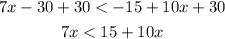
Subtracting 10x from both sides:

`\begin{gathered} 7x-10x<15+10x-10x \\ -3x<15 \end{gathered}`

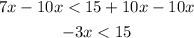
Finally, we need to divide by -3 but since -3 is a negative number, we change the symbol of the inequality as:

`\begin{gathered} (-3x)/(-3)>(15)/(-3) \\ x>-5 \end{gathered}`

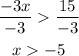
Therefore, the solution is x > - 5