Question

Darlene kicks a soccer ball off the ground and in the air, with an initial velocity of 34 feet per second. using the formula h(t) = −16t2 vt s, what is the maximum height the soccer ball reaches?

17.7 feet
18.1 feet
19.3 feet
20.2 feet

Answer 1

18.1 is the answer. I am glad I could help.

Answer 2

The maximum height of ball is 18.1 feet. Option 2 is correct.

Explanation:

The height of the soccer ball is defined by the formula,

`h(t)=-16t^2+vt+s`

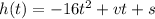
Where, v is initial velocity and s is initial height of ball.

It is given that initial velocity is 34 feet per second and the initial height of ball is 0.

`h(t)=-16t^2+34t`

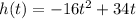
The leading coefficient is negative, so it is a downward parabola. The vertex of a downward parabola is point of maxima.

The vertex of a parabola
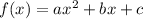`f(x)=ax^2+bx+c` is

`((-b)/(2a),f((-b)/(2a)))`

`(-b)/(2a)=(-34)/(2(-16))=1.0625`

`h(1.0625)=-16(1.0625)^2+34(1.0625)=18.0625\approx 18.1`

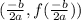
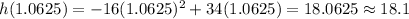
Therefore the maximum height of ball is 18.1 feet. Option 2 is correct.