Question

Mrs. Matthews wants to have $18,000 in the bank in 2 years. If she deposits $9000 today at 6% compounded quarterly for 2 years, how much additional money will she need to reach the desired $18,000?

Answer 1

depends if you want
1. find how much he will earn, find the differnce between that and 18000
2. see how much to invest till he will get 18000


A=
`P(1+ (r)/(n))^(nt)`

A=futre amount
P=present amout
r=rate in decimal
n=number of times per year ccompounded
t=time in years


1.
A=?
P=9000
r=0.06
n=4 (quarter means 4 times per year)
t=2
?=
`9000(1+ (0.06)/(4))^((4)(2))`
?=
`9000(1+ 0.015)^(8)`
?=
`9000(1.015)^(8)`
?=10138.4 will be earned
18000-10138.4=7861.6 needed

2.
A=18000
P=9000+x
r=0.06
n=4 (quarter means 4 times per year)
t=2
18000=
`(9000+x)(1+ (0.06)/(4))^((4)(2))`
18000=
`(9000+x)(1+ 0.015)^(8)`
18000=
`(9000+x)(1.015)^(8)`
divide both sides by 1.015^8
15978.8=9000+x
minus 9000 both sides
6978.8 needed




if he willnot be investing any more, he needs $7861.6 more
if he will invest more he will need to invest $6978.8 more

Answer 2

She needs additionally 7,861.57 to reach the desired 18,000.

Explanation:

Compounded interest formula is

`A=P(1+(r)/(n) )^(nt)`

Where
`P` is the principal,
`r` is the interest rate in decimal number,
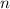`n` is the number of compounded periods within a year and
`t` is time in years.

By given, we have

`P=9,000\\t=2\\n=4\\r=0.06`

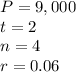
Replacing all values, we have

`A=P(1+(r)/(n) )^(nt)\\A=9000(1+(0.06)/(4) )^(4(2))= 9000(1.015)^(8)\\ A=10138.43`

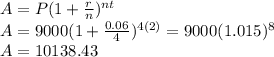
After 2 years, Mrs. Matthews will have 10,138.43.

So, the difference she needs to reach 18,000 is

`-10,138.43+18,000=7,861.57`

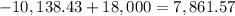
Therefore, she needs additionally 7,861.57 to reach the desired 18,000.