Answer:
Range is y ≥ –11
Explanation:
This is quadratic equation.
A quadratic equation's range can be found if we find the vertex.
For quadratic equations that have a positive number in front of
 , it is upward opening and thus all the numbers greater than or equal to the minimum value of vertex is the range.
, it is upward opening and thus all the numbers greater than or equal to the minimum value of vertex is the range.
The formula for vertex of a parabola is:
Vertex =

Where,
 is the coefficient of
is the coefficient of

 is the coefficient of
is the coefficient of

From our equation given,
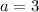 and
and

Now,
 coordinate of vertex is
coordinate of vertex is

 coordinate of the vertex IS THE MINIMUM VALUE that we want. We get this by plugging in the
coordinate of the vertex IS THE MINIMUM VALUE that we want. We get this by plugging in the
 value [
value [
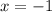 ] into the equation. So we have:
] into the equation. So we have:

Hence, the range would be all numbers greater than or equal to

Third answer choice is the right one.