Question

Identify the axis of symmetry and the vertex of the function. y=-5x^2+x+4

Answer 1

The general equation of parabole with vertex (h,k) is,

`y=a(x-h)^2+k`

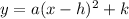
Simplify the equation to obtain in standard form equation.

`\begin{gathered} y=-5x^2+x+4 \\ =-5(x^2-(x)/(5))+4 \\ =-5(x^2-2\cdot(1)/(10)\cdot x+(1)/(100)-(1)/(100))+4 \\ =-5(x-(1)/(10))^2+(1)/(20)+4 \\ =-5(x-(1)/(10))^2+(81)/(20) \end{gathered}`

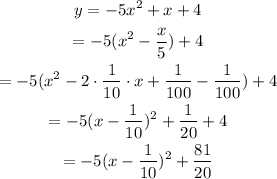
On compare equation, the vertex is (1/10,81/20).

The axis of symmetry for the standard function is x = h. So axis of symmetry for the function is,

`x=(1)/(10)`

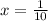
Answer:

Vertex: (1/10,81/20) or (0.1,4.05)

Axis of symmetry: x = 1/10 or x = 0.1