The general equation of parabole with vertex (h,k) is,
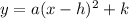
Simplify the equation to obtain in standard form equation.
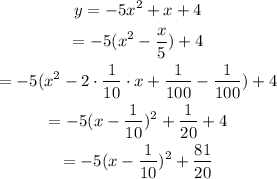
On compare equation, the vertex is (1/10,81/20).
The axis of symmetry for the standard function is x = h. So axis of symmetry for the function is,
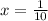
Answer:
Vertex: (1/10,81/20) or (0.1,4.05)
Axis of symmetry: x = 1/10 or x = 0.1