Answer:
The range of the square's side is between 0 and 10 meters.
Explanation:
The area of a square is defined as:
Area = x*x
Where x is the length of the square's side. It also could be writing as:
Area =

Then, the question say that the area is less than 100 m^2, which means that the area have a value below 100 m^2. This is equivalent to write:
Area <
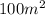
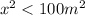
Now we can solve for x and obtain:
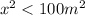
![x<\sqrt[2]{100m^(2)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/6qbevi4k9gudw59sjdvh4ybt6bwg5s24uw.png)
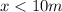
Finally for getting a reasonable range for the square's side is logic to use a positive number and a number that also fulfill with this last condition (x<10m).
So, the range for the square's side is number greater than zero and smaller than 10 meters. It also could be writing as: (0,10)