Question

A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5 points. If x is the number of 3-point questions and y is the number of 5-point questions, the system shown represents this situation. x + y = 24 3x + 5y = 100

Answer 1

Let the value of 3-points questions be x.
The value of 5-point questions be y.
x + y = 24
Then x = 24 - y which makes 3x + 5y = 100
3(24 - y) + 5y = 100
72 - 3y + 5y = 100
Lets get the ys together, 72(-3y + 5y) = 100
72 + 2y = 100
The value of y = (100 - 72) = 2y
2y = 28
y = 14.
If y is equal to 14, what about x?
x = 24 - y
x = 24 - y
x = 24 - 14
x = 10.
The value of 3-points questions is 10, and the value of 5 points questions is 14.

Answer 2

Let x be the number of 3- point questions and y be the number of 5-points questions.

As per the given statement:

A science test, which is worth 100 points, consists of 24 questions.

Then the system of equation is:

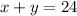`x + y = 24` ......[1] and

3x + 5y = 100 ......[2]

we can write equation [1] as ;

y = 24 -x

Substitute this in equation [2] we have;

`3x + 5(24-x) = 100`

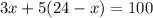
Using distributive property:
`a\cdot (b+c) = a\cdot b +a \cdot c`

3x + 120 - 5x =100

Combine like terms:

120 - 2x =100

Subtract 120 from both sides we get;

120 -2x -120 = 100-120

Simplify:

-2x = -20

Divide both sides by -2 we get;

`(-2x)/(-2)= (-2)/(-2)`

Simplify:

x = 10

Substitute the value of x in equation [1] to solve for y;

10 + y =24

Subtract 10 from both sides we get;

10 + y -10 = 24-10

Simplify:

y = 14

Therefore, the number of 3-points questions x is, 10 and the number of 5-points questions y is, 14