Question

some of the steps in the derivation of the quadratic formula are shown. step 3: –c b^2/4a=a(x^2 b/ax b^2/4a62) step 4a: –c b^2/4a=a(x b/2a)^2 step 4b: -4ac/4a b2/4a=a(x b/2a)^2 which best explains or justifies step 4b? -factoring a polynomial -multiplication property of equality -converting to a common denominator -addition property of equality

Answer 1

Answer: (c) converting to a common denominator.

Step-by-step explanation: Our quadratic equation
`ax^(2) +bx+c=0,~a\\eq 0` can be solved as follows -

`ax^(2) +bx+c=0\\\\\Rightarrow x^(2) +(b)/(a)x+(c)/(a)=0,~\textup{since}~a\\eq 0\\\\\Rightarrow x^(2) +(b)/(a)x=-(c)/(a)\\\\\Rightarrow x^(2) +2* (b)/(2a)+(b^2)/(4a^2)=(b^2)/(4a^2)-(c)/(a)\\\\\Rightarrow (x+(b)/(2a))^2=(b^2-4ac)/(4a^2)\\\\\Rightarrow x+(b)/(2a)=\frac{\pm\sqrt {b^2-4ac}}{2a}\\\\\Rightarrow x=(-b\pm√(b^2-4ac))/(2a).`

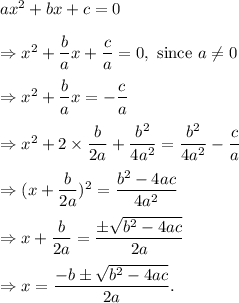
So, according to the given information, the step 4b explains the process of conversion of the terms on both sides to make the denominators same.

Thus, the correct option is (c) converting to a common denominator.

Answer 2

-converting to a common denominator

The terms -c of the left side was converted to -4ac/4a to have the same denominator of b^2/4a.