Question

Which statements are true for the function y = |x| - 2? Select all that apply.

The value of the function is never negative.
Its graph has a V-shape.
There is only one input for which the output is 0.
There are two inputs for which the output is 5.
The vertex of its graph is at (0, -2).

Answer 1

Two last answers are correct

Answer 2

Answer: The correct options are,

Its graph has a V-shape.

There are two inputs for which the output is 5.

The vertex of its graph is at (0, -2).

Explanation:

Here, the given function is,

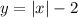`y=|x|-2` ------(1)

Which is an absolute function,

Since, the graph of an absolute function is always V shaped,

⇒ The graph of the given function is V-shaped,

Also, the range of the function is
`[-2, \infty)`

So, the value of the function can be negative,

Now, for y = 0,

`\implies 0 = |x|-2`

`\implies |x|=2\implies x =\pm 2`

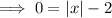
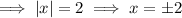
Thus, there are two inputs for which the output is 0,

Also, for y = 5,

`\implies 5=|x|-2`

`\implies |x|=7\implies x = \pm 7`

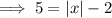
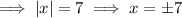
Thus, there are two inputs for which the output is 5,

Since, if an absolute function is,

`y=a|x-h|+k` ------(2)

Then, the vertex of the function is (h,k),

By comparing equation (1) and (2),

The vertex of the given function is, (0, -2 )