Question

what is the range of the function g(x) = |x – 12| – 2? a). y > –2 b). y c). y > 12 d). y

Answer 1

`\left \ y`

Explanation:

The function is given by
`g(x)=|x-12|-2`

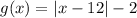
It is an absolute value function which has a v- shaped graph.

The vertex form of an absolute function is given by y = a|x-h| +k, where (h,k) is the vertex.

Comparing the given equation with this, we have

h = 12

k = -2

Hence, the vertex would be (12,-2).

Now, the range of the function is the set of y values for which the function is defined.

This function has vertex of (12,-2). hence, it would not be take any values which are less than -2. Please see the attache graph.

Hence, the range would be the all y values greater than or equal to -2.

Hence, range is given by
`\left \y\geq -2 \right \`