Question

the function h(x) is quadratic and h(3) = h(–10) = 0. which could represent h(x)? h(x) = x2 – 13x – 30 h(x) = x2 – 7x – 30 h(x) = 2x2 26x – 60 h(x) = 2x2 14x – 60

Answer 1

`h(3)=h(-10)=0\\\\therefore\\\\h(x)=a(x-x_1)(x-x_2)\\\\h(x)=a(x-3)(x+10)=a(x^2+7x-30)\\\\Answer:\boxed{h(x)=x^2+7x-30}`

Answer 2

`h(x) = 2x^2+14x - 60`

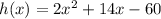
Explanation:

`h(3) = h(–10) = 0`

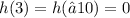
h(3) means x=3

h(-10) means x=-10

Plug in x values and find out h(3) and h(-10)

LEts check with each option

`h(x) = x^2 - 13x - 30`

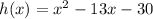
`h(3) = 3^2 - 13(3) - 30=-60` h(3) is not equal to 0

LEts check with option B

`h(x) = x^2 - 7x - 30`

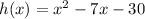
`h(3) = 3^2 - 7(3) - 30=0` h(3) is not equal to 0

option C

`h(x) = 2x^2 +26x - 60`

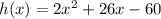
`h(3) = 2(3)^2+26(3)-60=36` h(3) is not equal to 0

option D

`h(x) = 2x^2+14x - 60`

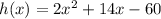
`h(3) = 2(3)^2+14(3)-60=0` h(3) is equal to 0

Plug in -10 for x

`h(3) = 2(-10)^2+14(-10)-60=0` h(-10) is equal to 0