Given:
Time it takes the pipe to fill the pool = 8 hours
Time it takes to drain the pool = 20 hours
Let's find the time it will take the pipe to fill the pool if the drain is left open.
We have the rates as:
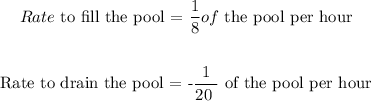
To find the time it will take to fill if the drain is left open, we have the equation:
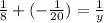
Where y represents the time it will take to fill the pool if the drain is left open.
Let's solve for y.
We have:
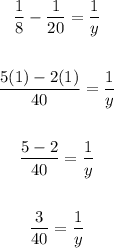
Cross multiply:
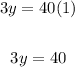
Divide both sides by 3:
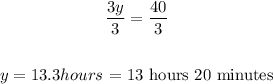
Therefore, if the drain is left open, it will take 13.3 hours for the pipe to fill the pool.
ANSWER:
13.3 hours