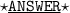
a) (x-3)2 +(y-17) 2 = 25
b) 11.07
c) T7/6 radians
Explanation:
a) The center of the circle is the midpoint
of the given segment, so is ...
A (P +Q)/2 = (8, 17) +(-2, 17)/2 = (6, 34)/
2= (3, 17)... center
center and end coordinates: 8-3 = 5.
The radius is the difference between
The equation of a circle with center (h, k)
and radius r is ...
x-h 2 + -k^2 = r^2
(x-3)2 +(y -17) 2 = 25
This circle's equation is
________
b) The length of the arc is given by ..
S = re
where r is the circle radius and e is the
We can find the central angle using a little
trigonometry. Point R differs from point A
by
R-A (0, 13)-(3, 17) = (-3,-4)
center of the circle. The sine of this angle
QAR is 4/5, so its value is..
so is 4 units below and 3 units left of the
angle QAR = arcsin(4/5) = 53.13
Then angle PAR is the supplement of this,
so about 126.87 , or 2.2143 radians. Then
the arc length is..
S = (5)(2.2143 radians)
s 11.07
________
c) The area of a sector is given by ..
A = (1/2)r2.0
Then the angle is ..
= (2A)/2
For the given values and r=5, we have..
2(25/12m)/25
T/6
central angle of m/6 radians, or 30°.
The sector with that area will have a