Question

The ordered pairs below represent a relation between x and y.(-3,1), (-2,3), (-1,5), (0,7), (1,9), (2,11)Could this set of ordered pairs have been generated by a linear function?A. No, because the distance between consecutive y-values is different than the distance between consecutive x-valuesB. Yes, because the distance between consecutive x-values is constantC. Yes, because the relative difference between y-values and x-values is the same no matter which pairs of (x, y) values you use to calculate itD. No, because the y-values decrease and then increase

Answer 1

yes because its like x cant cheat on y but y can cheat on x so basically your answer is yes and if you  need anything else let me know 

Answer 2

The correct answer is C.

Explanation:

Notice that the difference between consecutive values of x is always 1, and the difference between consecutive values of y is always 2. This means that

`(x_(1)-x_(0))/(y_(1)-y_(0)) = 2`

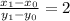
where
`x_0` and
`x_1` stands for two consecutive values of x, and the same goes to y.

Now, notice that this is the definition of the slope of the equation of a line. Then, a line can be characterized by this condition, and that is why C is the correct answer.

Anyway, you can check that this set of point is generated by a linear function in other way. Suppose that it can be done, and the linear function has the form

`y=mx+n`.

From the pair (0,7) we deduce that
`7 =m*0+n`, then
`n=7`. Now, substituting the pair (-3,1) we get
`1=-3*m+7` and as consequence
`m=2`. Thus, if the points are generated by a linear function, its expression would be
`y=2x+7`.

Now, substitute the different values of x and check that the same values of y are obtained.