Question

The statement tan theta -12/5, csc theta -13/12, and the terminal point determined by theta is in quadrant 3."

A. cannot be true because 12^2 + 5^2 does not equal 1.
B. cannot be true because if tan theta = -12/5, then csc theta = plus or minus 13/5.
C. cannot be true because tan theta must be less than 1.
D. cannot be true because tan theta is greater than zero in quadrant 3.

Answer 1

The answer would be D. Cannot be true because tan theta is greater than zero in quadrant 3.

Answer 2

Option D is correct.

The given statement cannot be true because tan theta is greater than zero in quadrant 3.

Step-by-step explanation:-

In quadrant 3rd ,

Cosine and Sine both are negative and tangent is positive.

As per the statement:-

The terminal point determined by theta is in quadrant 3.

Given:-

`\tan \theta =(-12)/(5)`

`\csc \theta = (-13)/(12)`

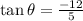
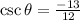
Since,
`\theta` is in quadrant 3,

⇒
`\tan \theta` cannot be negative.

Therefore, the given statement cannot be true because tan theta is greater than zero in quadrant 3.