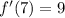Question

Find the derivative of f(x) = 9x + 5 at x = 7.

Can someone please show me a simple way to do this o_O

Answer 1

The derivative of a variable raised to exponent of n, x^n is equal to the product of n and x raised to exponent of n-1.
d(x^n) = (n)(x^n-1)
So, from the given
d(9x + 5) = (1)(9x^1-0) + 5(0)
= 9
The given value of x is irrelevant to this item because the derivative does not contain any variable x.

Answer 2

The derivative of f(x) = 9x + 5 at x = 7 is:

`f'(7)=9`

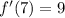
Explanation:

The derivative of a function is the rate of change of the dependent variable i.e. y=f(x) with respect to the independent variable i.e. x.

The derivative of the function f(x) is given by:

`f'(x)=(df)/(dx)`

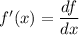
Now, we know that:

`(d)/(dx)x=1\\\\\\and\\\\\\(d)/(dx)c=0`

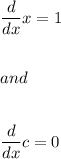
where c is a constant term.

Here we have the function f(x) as:

`f(x)=9x+5`

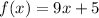
Hence,

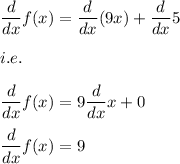
`(d)/(dx)f(x)=(d)/(dx)(9x)+(d)/(dx)5\\\\i.e.\\\\(d)/(dx)f(x)=9(d)/(dx)x+0\\\\(d)/(dx)f(x)=9`

i.e.
`f'(x)=9`

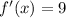
Also, when x =7 we have:

`f'(7)=9`