Question

The half-life of tritium, or hydrogen-3, is 12.32 years. After about 24.6 years, how much of a sample of tritium will remain unchanged?

A. 1/8
B. 1/4
C. 1/3
D. 1/2

Answer 1

The amount of the substance left after sometime, t, is given by the equation,
At = (Ai) x e^-kt
where Ai is the initial amount and k is constant. From the given half-life,
At / Ai = 0.5 = e^-k(12.32) ; k = 0.5626
Then, for the next set,
At/Ai = e^(-0.5626)x24.6 =
Thus, the answer is letter B.

Answer 2

Answer: The correct option is B.

Explanation: This is an example of radioactive decay and all the radioactive decay processes follow First order of kinetics.

Expression for the half life of first order kinetics is:

`t_(1/2)=(0.693)/(k)`

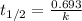
We are given:

`t_(1/2)=12.32years`

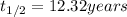
Putting in above equation, we get:

`12.32=(0.693)/(k)\\k=0.05625year^(-1)`

Expression to calculate the amount of sample which is unchanged is:

`N=N_oe^(-kt)`

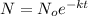
where,

N = Amount left after time t

`N_o` = Initial amount

k = Rate constant

t = time period

Putting value of k = 0.05625 and t = 24.6 in above equation, we get:

`N=N_oe^(-0.05625* 24.6)`

`(N)/(N_o)=0.25`

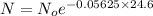
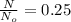
The above fraction is the amount of sample unchanged and that is equal to
`(1)/(4)`

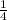
Hence, the correct option is B.