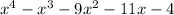Question

Write a polynomial equation of degree 4 that has the following roots: -1 repeated three times and 4

Answer 1

The polynomial is:

`x^4 - x^3 - 9x^2 - 11x - 4`

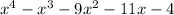
Explanation:

We are given roots of a polynomial as: -1, -1, -1, 4

We have to find the polynomial.

(x + 1)(x + 1)(x + 1)(x - 4) = 0

on multiplying first and second term and third and fourth term,we get

`(x^2 + 2x + 1)(x^2 - 3x - 4) = 0\\x^2(x^2 - 3x - 4) + 2x(x^2 - 3x - 4) + 1(x^2 - 3x - 4) = 0\\x^4 - 3x^3 - 4x^2 + 2x^3 - 6x^2 - 8x + x^2 - 3x - 4 = 0\\x^4 - x^3 - 9x^2 - 11x - 4 = 0`

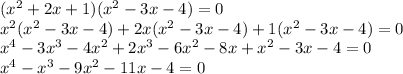
Hence, the polynomial is:

`x^4 - x^3 - 9x^2 - 11x - 4`

Answer 2

roots = -1, -1, -1, 4
(x + 1)(x + 1)(x + 1)(x - 4) = 0
(x^2 + 2x + 2)(x^2 - 3x - 4) = 0
x^2(x^2 - 3x - 4) + 2x(x^2 - 3x - 4) + 2(x^2 - 3x - 4) = 0
x^4 - 3x^3 - 4x^2 + 2x^3 - 6x^2 - 8x + 2x^2 - 6x - 8 = 0
x^4 - x^3 - 8x^2 - 14x - 8 = 0