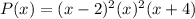Question

The polynomial of degree 5, P(x) has leading coefficient 1, has roots of multiplicity 2 at

x=2 and x=0, and a root of multiplicity 1 at x=-4
Find a possible formula for P(x)

Answer 1

yes, this is fun

remember the roots of a polynomial is
P(x)=(x-r1)(x-r2)...(x-rn)


so we have 5th degreee, means all exponents shoud add to 5

leading coeficient of 1, that means
P(x)=1x^n+bx^(n-1)...zx^0
means highest power coefience it 1

roots of multiplicity 2 at x=2 and x=0, means those roots show up 2 times each
root at x=2 means (x-2), it has multiplicity 2 so (x-2)^2
root at x=0 means (x-0), it has multiplicyt 2 so (x-0)^2

last one, multiplicity 1 and root at x=-4
(x-(-4))^1=(x+4)


so the polynomial is

`P(x)=(x-2)^(2)(x)^(2)(x+4)`